宋翠玉,张之辉
地球自转及绕太阳公转的轨道参数(偏心率、斜率和岁差)不是一成不变的,而是发生准周期性变化,例如,地轴的斜率以~4.1万年为周期在22.2-24.5度之间变化。这些轨道参数的变化引起地球接收的日照量发生变化,影响大气环流位置,引起气候带在纬度上的移动。气候进一步影响许多参数,这些参数直接或间接地影响沉积物的产生、运移和积累等过程[1],这些信息将被记录在地层之中(图1)。地层中由地球轨道驱动造成的旋回性记录称为米兰科维奇旋回[2],简称米氏旋回。在海相、陆相沉积记录中不断揭示出来的米氏旋回,为研究地质年代学、古气候-古环境演化、地质事件驱动机制等众多地球科学问题做出了重要贡献。
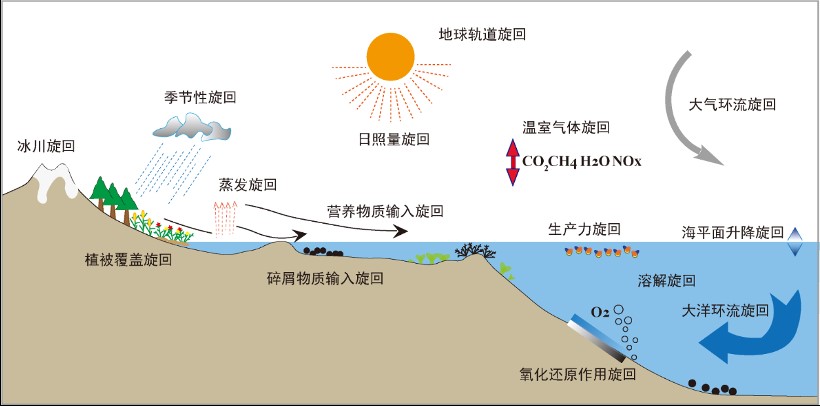
图1 由地球轨道周期引起的地球表层系统的旋回过程(据[1]改)
随深度变化的沉积剖面记录了特定地史阶段的古气候/古环境信息,实质上具有时间含义。不管是将岩性岩相特征直接数字化,生成诸如特殊岩石的颜色变化等数据,还是测量地层的物理/化学性质获得如自然伽马值(GR)/元素含量等古气候替代指标,均可以构建包含地层环境信息的时间(深度)序列,利用数学变换可以对这些沉积序列进行分析[3],建立(浮动)天文年代标尺。不断发展和完善的时间序列分析方法促进了米氏旋回分析向客观性、定量化方向发展[4]。
基于时间序列分析的米氏旋回研究流程可以简化为一个带有输入和输出的“黑匣子”。沉积记录中的参数序列(古气候替代指标)作为输入,输出(浮动)天文年代标尺。黑匣子内部主要包括数据预处理、频谱分析、天文驱动检验和天文调谐等环节(图2)。

图2 米兰科维奇旋回时间序列分析流程
1 输入:不同替代指标对天文轨道驱动和非天文噪声的响应具有差异性
不同沉积序列蕴含着不同的地质信息,对米兰科维奇旋回信号的记录也有差异。用于米氏旋回研究的替代指标大致分为四类:直观岩性数据、地球化学数据、地球物理数据和古生物数据等。其中,GR测井测量沉积物中伽马射线的强度,可以敏感反映沉积物中的泥质含量,进而反映古气候和古环境的微小变化,是米氏旋回分析的理想数据[5]。在海相沉积地层中,ARM和Th/U可反映早三叠世的内陆风化作用,GR、K、U、Th、磁化率和非碳酸盐组分等指示陆源补给[5]。鉴于不同沉积序列数据对天文轨道驱动和非天文噪声的响应具有差异性,综合利用多种替代指标有助于建立天文年代标尺[6]。
2 揭秘“黑匣子”
2.1 预处理减少环境“噪声”
数据预处理是对原始数据进行的一系列初始处理。主要包括重采样、剔除异常值、去趋势和预白化等,其目的是尽量消除地层数据中的各种环境“噪声”[2]。
2.2 如何判断地质记录中是否含有米氏旋回周期信号?
(1) 频谱分析定位候选周期
周期是频率的倒数,寻找米氏旋回周期信号最直接的途径就是对深度域的沉积序列观测值进行频谱分析,即将地层序列的信号强度按频率顺序展开,使其成为频率的函数,进而识别出信号中(准)周期性的成分[2](图3b)。快速傅里叶变换(Fast Fourier Transform,FFT)、周期图法(Periodogram)和多窗谱分析法(Multi-Taper Method,MTM)等都是常用的频谱分析方法。不同频谱分析方法的算法不同,各有优缺点,但计算结果基本一致[2]。
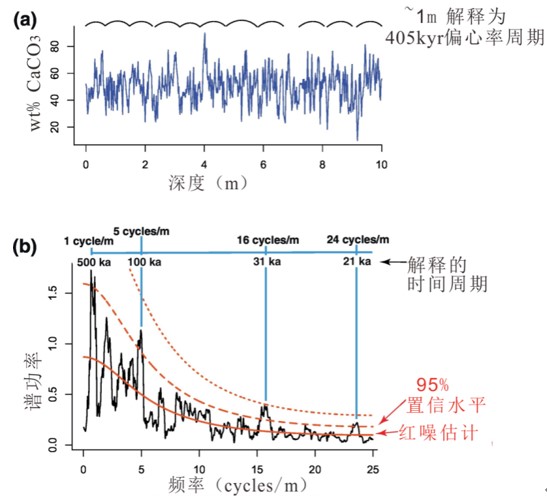
图3 频谱分析示例[7]
(a)10 m长的CaCO3质量百分比序列,采样间隔为0.02 m;(b)对(a)中数据的3π MTM频谱分析结果
(2) 噪声估计剔除随机噪声
通过频谱分析,可以获得数据中蕴含的一系列主周期信号,天文检验就是检验这些周期信号中是否包含受地球天文轨道驱动的米氏周期信号。然而,功率谱中的主周期(频率的倒数)信号既包含真实的米氏旋回信号,也包括一些无关的、随机出现的“噪声”。即使没有气候驱动参数(如日照量)的变化,气候系统中的各组成部分及其相互作用也会产生强烈的低频振荡[7],从而在低频谱段出现的能量较高的“红噪”(Red Noise)。因此,常采用一阶自回归模型(Auto Regressive Lag-1,AR1)估计沉积序列中红噪,生成红噪理论曲线并进行显著性检验,剔除峰值低于特定置信水平(如低于90%或95%)的频率(图3b)。
(3)检验是否天文驱动
在噪声压制后的功率谱中,判别峰值对应的频段组合是否由天文轨道驱动的方法主要有三种:比值法、调幅分析法和假设检验法。比值法较为直接,如果频谱分析获取的旋回周期之比与天文轨道参数的周期之比(长偏心率:短偏心率:斜率:岁差约为20:5:2:1)一致,则判定存在米氏信号。然而,由于受到噪声、频谱分析误差等影响,满足比例的频率组合可能不唯一。调幅分析法基于“长周期旋回对短周期旋回的天文调制现象”判别旋回是否受天文驱动,但长周期的振幅变化可能通过调谐和数据处理等过程人为地引入。假设检验法是基于统计学的方法,它先提出零假设,即假设筛选出来的频率都是与天文驱动无关的随机噪声,然后借助统计检验拒绝该假设,即可说明序列中存在米氏旋回信号。Meyers 和Sageman[8]提出的ASM方法、Li等[9]提出的eCOCO等方法中,均包含假设检验。
2.3 如何将深度域的地质记录赋予时间信息?
将识别出的米氏旋回信号调谐到理论的天文曲线上,使深度域的地层沉积序列变换到时间域,这一过程称为天文调谐,其目的是构建地层的年代模型(Age Model)。对于缺少年龄控制的地层而言,调谐只能建立浮动天文年代标尺,来计算地层或地质事件的持续时间。天文调谐方法可归纳为最小调谐法、统计法和反演法等三类(表1)。其中,统计法和反演法均为基于沉积速率定量估算的调谐方法。
表1 主要天文调谐方法列表
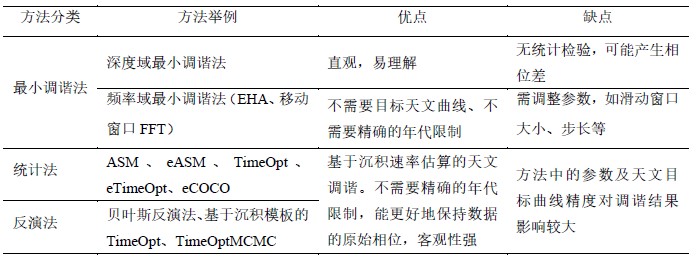
(1) 直观的最小调谐法
最小调谐法(Minimal tuning)使用最小数量的校准点将深度域序列曲线与时间域目标天文曲线联系起来完成校正,是最直观的调谐方法。实际操作中,为了更准确地定位校准点,常先将沉积序列曲线做带通滤波(Band Pass Filter)处理,选取滤波曲线的极小或极大值作为校准点。然而,该方法假定天文目标曲线正确,且没有利用统计法进行检验;当选取的目标曲线年代与真实数据年代不完全对应时,会产生相位差。
在缺少目标天文曲线的地史时期(如古生代),频率域的最小调谐往往获得理想效果。在滑动窗口上对地层数据序列做频谱分析,获得频率随深度变化的频谱图。在频谱图中追踪单个较连续的旋回信号(如长偏心率周期),生成沉积速率曲线。最后,根据沉积速率曲线生成年代模型进而将沉积记录变换到时间域(图4)。该类方法有EHA(Evolutive Harmonic Analysis)或改进的FFT[10]等。
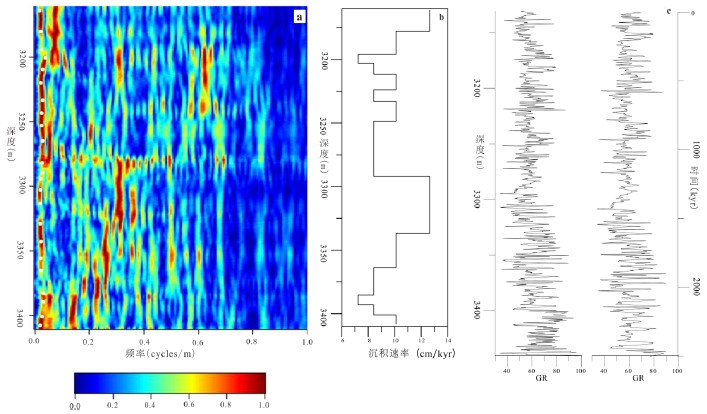
图4 频率域最小调谐法示意图
(a)EHA频谱,图中白点表示追踪到的405 kyr周期;(b)沉积速率曲线;(c)天文调谐结果
(2) 经典的统计法
统计法基于一系列可能的沉积速率,利用假设检验和蒙特卡洛模拟来估算最优沉积速率或追踪沉积速率的变化。这些方法不需要精确的年代限制,也能更好地保持数据的原始相位。ASM(Average Spectal Misfit,ASM)、eASM、TimeOpt(Time scale Optimization)、eTimeOpt(Evolutive Time scale Optimization)及eCOCO(evolutionary Correlation Coefficient)等都是统计法。
eCOCO基于一系列待“测试”的沉积速率,1)将古气候替代指标转换为时间序列,然后计算该时间序列的功率谱与天文解决方案功率谱之间的相关系数;2)记录对相关系数有贡献的天文参数的数量;3)使用蒙特卡洛模拟法对天文驱动信号进行零假设检验。最合适的沉积速率由高相关系数、多旋回信号及低零假设水平共同决定[9]。由于eCOCO采用了滑动窗口技术,可以跟踪替代指标沿地层序列在沉积速率上的变化(图5b、c、d深红色交集确定最优沉积速率曲线)。
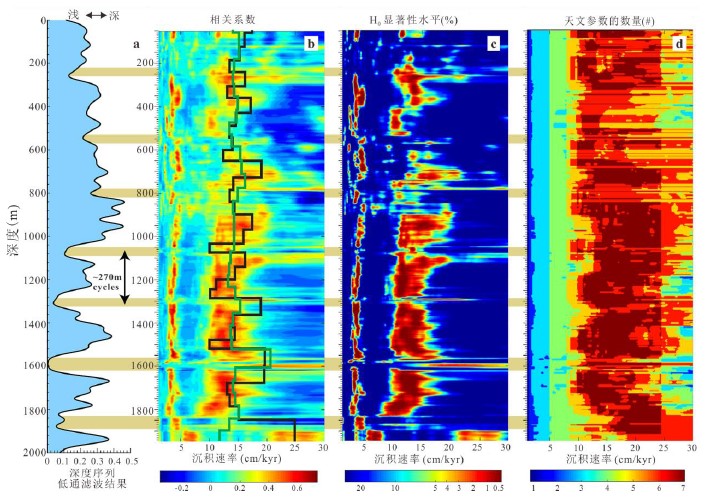
图5 晚三叠世Newark深度序列(0-2000 m)的eCOCO分析结果[9]
(a)深度序列的高斯低通滤波结果(截止频率为0.01 m−1),金色水平条为∼270 m旋回;(b)eCOCO相关系数图,黑线和绿线为已有的沉积速率研究结果;(c)零假设检验H0显著性水平图;(d)有贡献的天文参数数量变化图
(3) 基于模型的反演法
反演法将轨道调谐视作反演问题,一般先建立初始的沉积速率模型,然后借助贝叶斯公式等调整、优化模型,进而建立年代模型,主要有基于贝叶斯反演的天文调谐法[11]、基于沉积模板的TimeOpt反演法[7]和TimeOptMCMC(TimeOpt Markov Chain Monte Carlo)[12]法等。基于沉积模板的TimeOpt中,首先给定初始沉积速率模板,如阶跃变化模板(图6),在优化反演过程中,初始沉积模板与天文目标和数据动态交互调整,最终重建沉积速率曲线[7]。
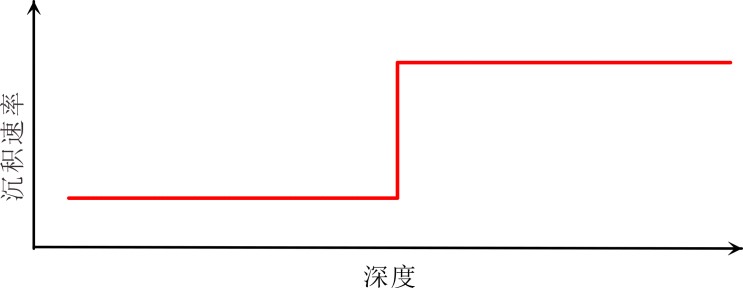
图6 阶跃变化的沉积模板示例[7]
3 旋回地层学分析相关的软件或工具包
基于时间序列分析的米氏旋回研究方法仍处在发展阶段,目前已经出现了一些较为成熟的软件或工具包,如AnalySeries、Astrochron[7]、Acycle[13]等。此外,还有一些较成熟的可用于频谱分析的工具包,如Past和Redifit等。其中,Acycle融合了多学者提出的时间序列分析方法,且其可视化界面友好,是旋回地层学分析的有力工具之一。
本文第一作者系山东科技大学讲师,第二作者为山东科技大学博士后。本文属作者认识,相关问题交流可通过邮箱scy57273@126.com与本人联系。欲知更多详情,请进一步阅读下列参考文献。
主要参考文献
[1] Strasser A., Hilgen F. J., Heckel P. H., 2006. Cyclostratigraphy - concepts, definitions, and applications. Newsletters on Stratigraphy 2006, 42(2):75-114.
[2] 吴怀春,张世红,冯庆来,等, 2011. 旋回地层学理论基础、研究进展和展望,地球科学——中国地质大学学报, 36(3):409- 428.
[3] Weedon G., 2003. Time-series analysis and cyclostratigraphy. Cambridge: Cambridge University Press
[4] 宋翠玉,吕大炜, 2022.米兰科维奇旋回时间序列分析法研究进展, 沉积学报, 40(2):380-395.
[5] Li M., Huang C., Ogg J., et al, 2019. Paleoclimate proxies for cyclostratigraphy: Comparative analysis using a Lower Triassic marine section in South China. Earth-Science Reviews 189:125-146.
[6] Ma C. & Li M., 2020. Astronomical time scale of the Turonian constrained by multiple paleoclimate proxies. Geoscience Frontiers 11(4): 1345-1352.
[7] Meyers S. R., 2019. Cyclostratigraphy and the problem of astrochronologic testing. Earth-Science Reviews 190:190-223.
[8] Meyers S. R. & Sageman B. B., 2007. Quantification of deep-time orbital forcing by average spectral misfit. American Journal of Science 307(5):773-792.
[9] Li M., Kump L. R., Hinnov L. A., et al., 2018. Tracking variable sedimentation rates and astronomical forcing in Phanerozoic paleoclimate proxy series with evolutionary correlation coefficients and hypothesis testing. Earth and Planetary Science Letters 501:165-179.
[10] Shi J., Jin Z., Liu Q., et al.,2018. Terrestrial sedimentary responses to astronomically forced climate changes during the Early Paleogene in the Bohai Bay Basin, eastern China. Palaeogeography, Palaeoclimatology, Palaeoecology 502:1-12.
[11] Malinverno A., Erba E., Herbert T. D.,2010. Orbital tuning as an inverse problem: Chronology of the early Aptian oceanic anoxic event 1a (Selli Level) in the Cismon APTICORE. Paleoceanography 25, PA2203, doi:10.1029/2009PA001769.
[12] Meyers S. R. & Malinverno A.,2018. Proterozoic Milankovitch cycles and the history of the solar system. Proceedings of the National Academy of Sciences of the United States of America 115(25):6363-6368.
[13] Li M., Hinnov L. & Kump L.,2019. Acycle: Time-series analysis software for paleoclimate research and education. Computers & Geosciences 127:12-22.







